Taking a closer look at the 5x5 magic square, Part One
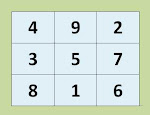
The 5x5 magic square
A closer look at the internal 3x3 grid within the 5x5 magic square
Concerning the blue colored numbers: 7, 14 and 18 sum to 39 as do 8, 12 and 19; 9, 12, and 18; and lastly 8, 14, and 17. When two of these groups of three numbers are connected by lines, this is the image:
The fact that there are nine ( a square number) prime numbers in the 5x5 magic square that sum to another square number (100) and that the sum of the prime numbers in just the cruciform portion of the magic square is 61 (part of the 11-60-61 Pythagorean triplet) is cause to take a closer look at the 5x5 magic square.
Examining this square will reveal insights into the School of Pythagoras and what is referred to as the “secret math”. Pythagoreans were understandably amused by Pythagorean triplets that satisfied the Pythagorean Theorem, dubbed the most important of all mathematical formulae as this was a formula that described space and was represented symbolically by the carpenter’s square. The carpenter’s square was also known as the gnomon.
The gnomon established a long tradition for thousands of years as an astronomical instrument that could identify summer and winter solstice and is forever linked as a model for time. Time, space, and math: these were the concepts that allowed humankind to evolve and prosper (via agriculture) and thus were also of great importance to Plato, Pythagoras, the early Chinese, and the early Christian hierarchy. Important symbols for these concepts have survived for thousands of years and are relevant, sometimes, to the understanding of early Christian art and architecture (see below). [for more on the gnomon, see Websters Dictionary and Needham’s Science and Civilisation in China, Vol. III p. 19-22].
The gnomon established a long tradition for thousands of years as an astronomical instrument that could identify summer and winter solstice and is forever linked as a model for time. Time, space, and math: these were the concepts that allowed humankind to evolve and prosper (via agriculture) and thus were also of great importance to Plato, Pythagoras, the early Chinese, and the early Christian hierarchy. Important symbols for these concepts have survived for thousands of years and are relevant, sometimes, to the understanding of early Christian art and architecture (see below). [for more on the gnomon, see Websters Dictionary and Needham’s Science and Civilisation in China, Vol. III p. 19-22].
The 5x5 magic square
The first point of interest is that this square features two Pythagorean Triplets that are in a gnomonic or right angle relationship, 5-12-13 and 7-24-25. This is the smallest order magic square in the Luo Shu format that features two Pythagorean triplets. Note that all the odd components of the two Pythagorean triplets fall within the cruciform of odd numbers.
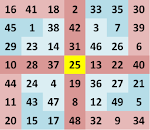
The second point of interest is the number 39. The above 5x5 magic square that is colored shows four groups of numbers in the corners of the square shaded in beige that are also in the shape of a gnomon or right angle. The total sum of the numbers shaded beige is 156; however, each gnomonic component sums to 39.
12
|
25
|
8
|
5
|
13
|
21
|
18
|
1
|
14
|
demonstrates that each column, row, and diagonal that pass thru the central axis (13) sums to 39.
Concerning the blue colored numbers: 7, 14 and 18 sum to 39 as do 8, 12 and 19; 9, 12, and 18; and lastly 8, 14, and 17. When two of these groups of three numbers are connected by lines, this is the image:
It was pointed out earlier that the total sum of all the prime numbers in the square is 100 and the total sum of the prime numbers in just the cruciform portion of the square is 61, the difference of these two numbers being….39.
The third point of interest concerns the sum total of each of the three groups of numbers identified by color. The sum total of the numbers shaded beige is 156, when divided by 13 gives us 12, and there are indeed twelve numbers that comprise this sum. The sum total of the numbers shaded light blue is 104, when divided by 13 gives us 8, and there are indeed eight numbers that comprise this sum. Lastly, the sum total of the numbers shaded bronze is 65, when divided by 13 gives us 5, and indeed there are five numbers that comprise this sum.
Math can be fun, or as my nephew says “cool”. (He did say weird at first but I corrected him). More relevant, this is how math was taught thousands of years ago.
Pythagoreans as well as the Chinese thousands of years prior to Pythagoras were interested in functional math that explained Time and Space. Things such as Pythagorean triplets, the gnomon, and calendrical numerology excited the Pythagoreans and the mathematically minded early Chinese; Luo Shu magic squares possessed all these characteristics and were part of the esoteric tradition of what some refer to as magic but was probably none other than math and wisdom.
More detailed explanations than can be given here are available in my book, NUMBER TIME ARCHETYPE Scroll to top of page, click on "a book for the library", and order for only $36.50 for the hardcover and $22.50 for the softcover.
The carpenter's square as a Christian Symbol
More detailed explanations than can be given here are available in my book, NUMBER TIME ARCHETYPE Scroll to top of page, click on "a book for the library", and order for only $36.50 for the hardcover and $22.50 for the softcover.
The carpenter's square as a Christian Symbol
Jesus and the four apostles, Ravenna mosaic - 7th century
The use of the "gammadia" symbol in early Christian art has raised some controversial issues, mainly that art historians throughout the ages have refused to acknowledge any meaning to this symbol and that its usage is strictly ornamental. The gammadia or carpenter's square is symbolic of the gnomon, time, space, and math. The gammadia's use on several hundred mosaics throughout Italy but especially in Ravenna over the course of five hundred years (between 350AD and 850AD) has been very consistent: the symbol only appears on clothing, altar cloths, or altar curtains to identify people or things of religious significance. The gammadia appears on the clothing of Jesus, the apostles, evangelists, and others who had status within the church. Furthermore, it is well documented that Popes during the Italian Renaissance had an obsession for Egyptian obelisks, another representation of the venerated gnomon. Therefore, the symbolic role of the gnomon and carpenter's square is consistent through out Christian art and architecture. Subjects such as the Christian use of symbols that relates to the early Chinese culture and their veneration of the Luo Shu are discussed in detail in my book.